
No último final de semana, a internet ficou encantada com tartarugas nadando em salas de estar e pandas gigantes sentados em sofás. É que caiu no gosto do povo um recurso do Google que permite que animais sejam vistos em 3D no ambiente em que os usuários estão.
A ferramenta funciona através de realidade aumentada, mesma tecnologia usada nos filtros interativos do Instagram - como o do vira-lata caramelo , por exemplo. Os animais em 3D do Google foram anunciados, na verdade, no Google I/O de 2019, mas o sucesso veio agora, depois que internautas começaram a comentar o recurso no Twitter.
Os animais podem ser encontrados através de uma busca simples no Google usando o celular. Em alguns modelos de smartphone, é possível apenas ver o bicho em 3D, sem inseri-lo no ambiente.
Leia também: Saiba como encontrar qualquer filtro no Instagram
Já em modelos mais atualizados, dá usar o recurso de realidade aumentada (RA) para posicionar o animal escolhido no seu ambiente. Para saber se seu celular Android tem suporte à tecnologia de RA, vá até a loja de aplicativos e procure pelo app Google Play Services RA, responsável por desbloquear experiências de realidade aumentada.
Se o aplicativo aparecer na busca, mantenha-o atualizado; se não, é porque seu smartphone não suporta a tecnologia. No caso do iOS, os modelos superiores ao iPhone 6S conseguem acessar o recurso.
O Google não divulgou uma lista completa de quais animais estão disponíveis para serem vistos em 3D, mas uma grande quantidade de opções pode ser encontrada.
Leia também: Google dá dicas para manter os pequenos negócios durante o isolamento
Tutorial: como ver os animais 3D do Google
- 1. Procure pelo nome de um animal no buscador do Google pelo celular;
- 2. No cartão de descrição do animal, desça até a animação;
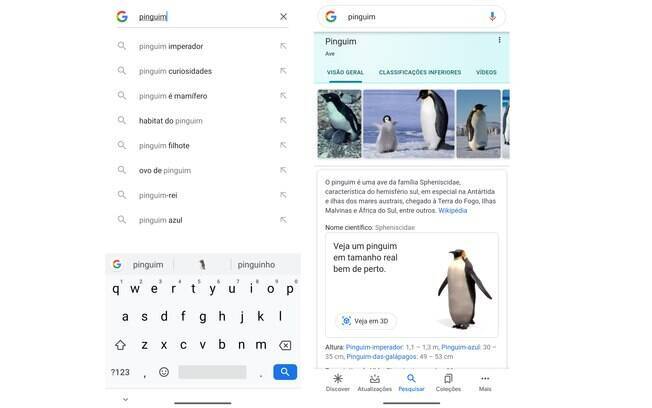
- 3. Clique em “veja em 3D”;
- 4. Nesta página, é possível interagir com o animal, vendo-o de todos os ângulos. Para colocá-lo no seu ambiente, clique em “veja no seu espaço”;
- 5. Pronto! Na tela que surgir, dá para ver o animal em tamanho real e de todos os ângulos possíveis.
